Fifteen Essays

Constructive Collisions

Boston, MA

Studio J. Jih, Summer Research

Collaborator: Inez Ow
Research Supervisor: J. Jih

What happens when idealized digital geometry meets material reality?

Fidelity of digital space and real space are often misaligned. In practice, these discrepancies lead to project setbacks and design failures. Constructive Collisions is a set of fifteen studies, exploring the productive friction between infinitely precise geometry, and real physical and spatial constraints of material and joinery tolerances.

Detail View: Spiral Chainlink applied to cylindric surfaces.

Premise Diagram: Tectonic System X Surface Geometry

The research premise begins with a generative design matrix. Three typical families of tectonic systems are selected: Membranes (monolithic continuous surfaces), Plates (discrete surfaces), and Sticks (linear members). Five typical families of surfaces are selected, Ruled, Toroidal, Spherical, Conic, and Cylindric. For each surface geometry, a specific instance is selected as a control variable (ex: the Conoid as an instance of ruled surface). Over the course of two months, we designed and prototyped parametric schemes for each square in the matrix.

Each physical study fits within a bounding box of approximately 8” x 8” x 8”. Through these investigations, we realize that there is an inextricable link between the labor of design and the labor of execution. The architect has agency to take a stance with their design decision-making. They can select more harmonious resolutions of geometry and material to ease the difficulties of construction, or lean into the discord to produce new generative outcomes from standard systems.

Fifteen Essays

How do materials account for incremental change?

Though constructed from straight ruling lines, the conoid presents a challenge to discretize due to the incremental change in orientation. In the case of standing seam metal panels, this change is incorporated into custom profiles and fold patterns, whereas the stretch fabric of a membrane system accounts for the same degree of change with comparatively little customization necessary.

[Membrane X Conoid]
Pleated stretch fabric meets ruled surface.

[Plate X Conoid]

Standing seam brass meets ruled surface.

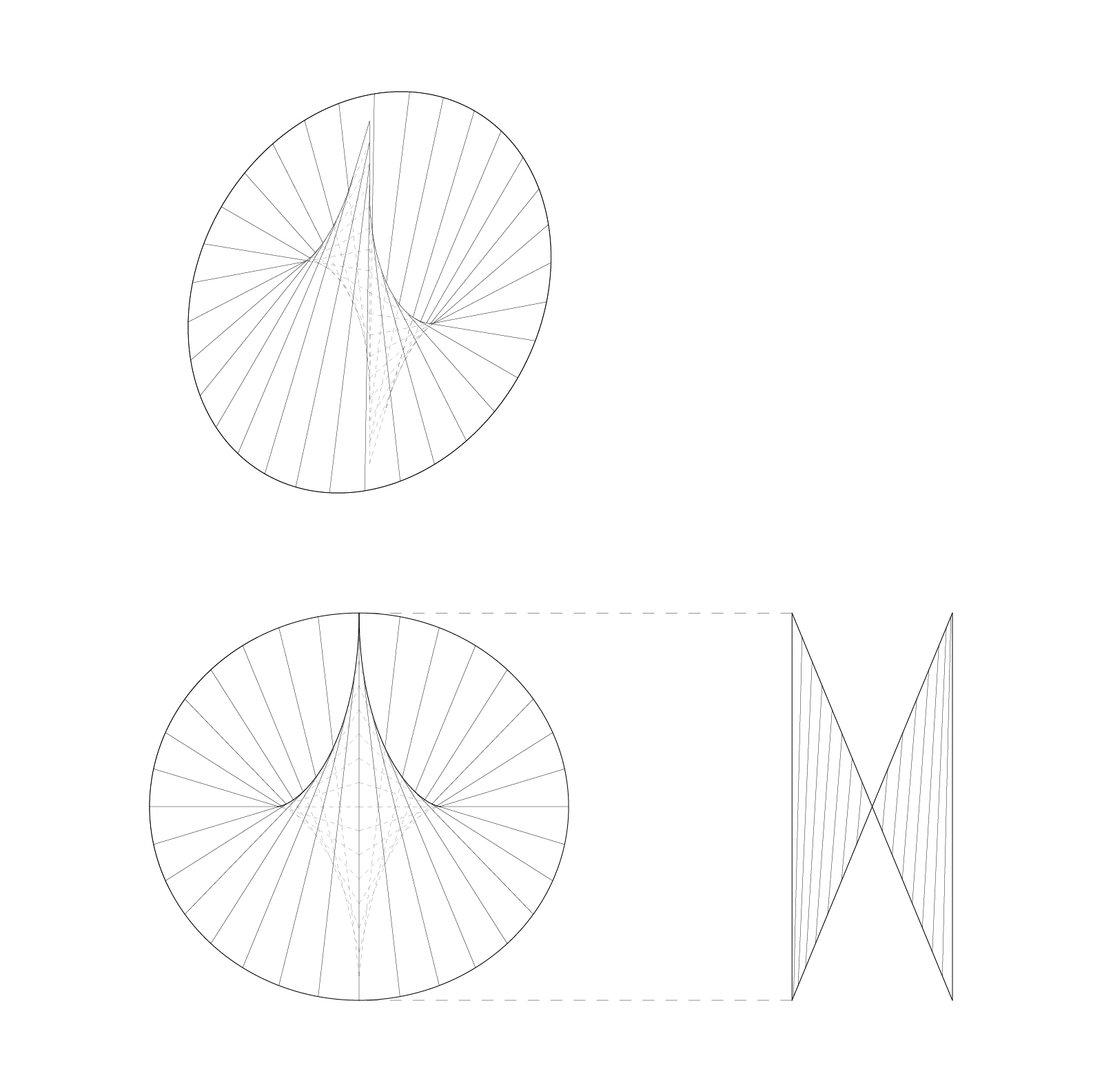
Can we build nonuniform double curvature with a single piece of material?

The cyclide is constructed by revolving a circular profile about an origin point. This operation results in a toroidal surface, in which the double curvature is nonuniform across the geometry. To build the surface, we need to look at the moment of tightest tolerance: the inner ring of the cyclide.

[Stick X Cyclide]
Rattan strip meets toroidal surface.

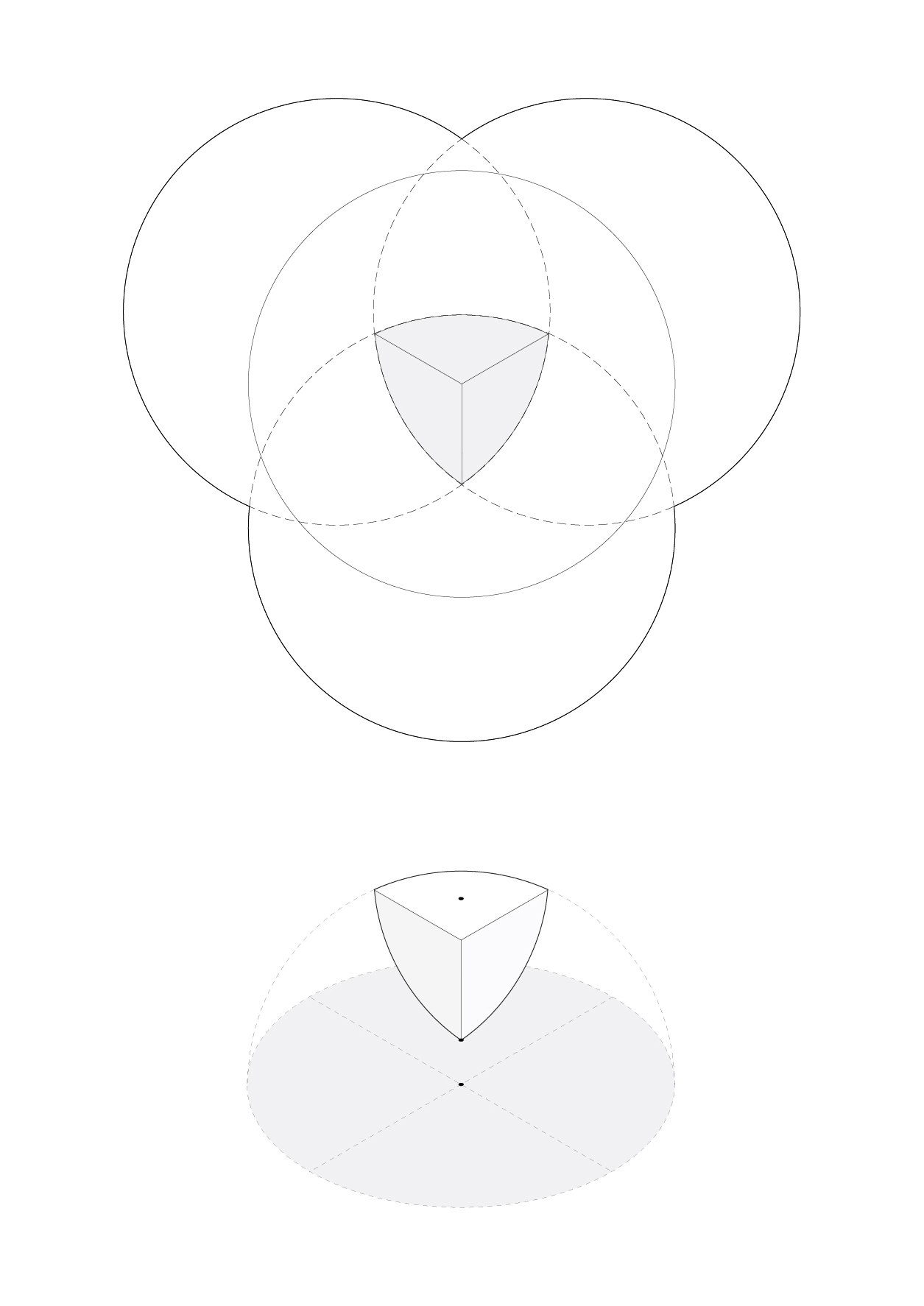
Can we impart “sidedness” on a spherical surface?

The established strategy for constructing a sphere of flat sheets would be to discretize the sphere into triangular panels, as in a geodesic dome. Approaching this model, we wanted to see if we could apply a less homogenous strategy. Here, the surface is approximated using developable strips. Alternating between transparent and opaque strips, the sideness of the split rivet fastener is exposed, creating two opposed readings of the object.

[Plate X Reuleaux] Split-riveted plastic strips meet spherical surfaces.

Transparent Orientation

Opaque Orientation

Can we use orientation to transform the reading of a conic surface?

To create a conic surface from stick members, the key decision comes from whether to orient the stick tangent or perpendicular to the surface. Though linear members are effective for realizing the straight isocurves of a cone, they do not inherently resolve the convergence at the top of the cone. Here, we explore a perpendicular orientation to the surface: using strands of fiberoptic cable as a thatch to create the surface without gaps. However, in the process of orienting strands, the entire constructed surface is offset in space, and rupture in the surface emerges where the side of the strands are revealed.

[Stick X Sphericon]
Fiberoptic thatch meets conic surfaces.

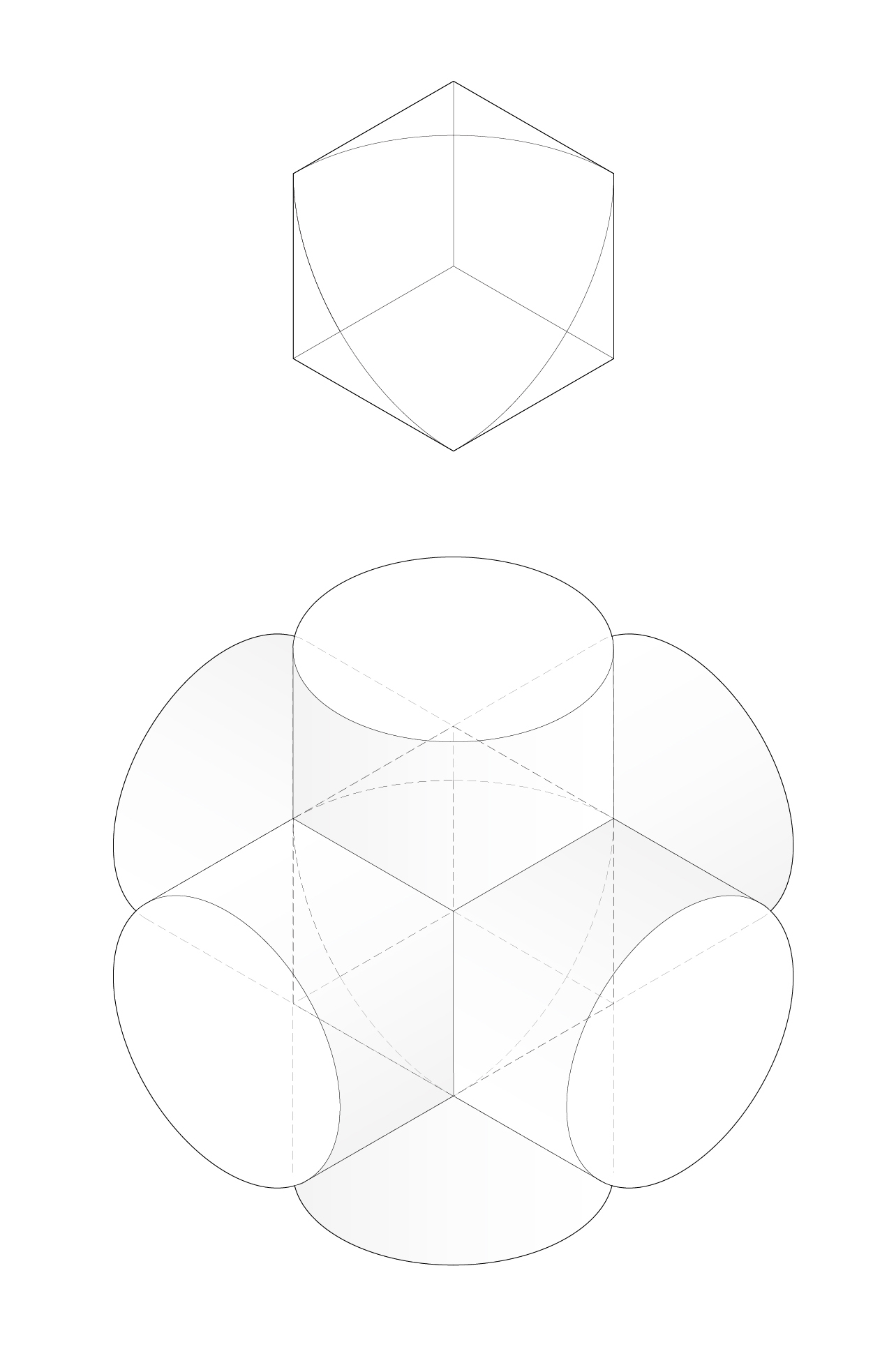
Can we build cylinders as flexible membranes?

A cylinder presents a unique challenge for a membrane. Though many membrane-like materials can be stretched over a cylindric frame, most will droop significantly in the middle of the span, approximating a minimal surface, not a cylinder. Being straight in one direction and curved in the other, the cylinder requires a material with unilateral stability. To resolve this constraint, we rely on the assembly process of chainlink: individual spirals are woven together in series to create a mesh. Each spiral exhibits self-rigidity in the long direction, but only loosely interlocks with the adjacent spiral, allowing for flexibility in the short direction.